The size of a tree is the size of the root. The size of a node is the number of descendants it has including itself. Therefore, the tree size is the number of all tree nodes.
The height (or depth) of a tree is the length of the path from the root to the deepest node in the tree. A (rooted) tree with only one node (the root) has a depth of zero. Conventionally, an empty tree (tree with no nodes, if such are allowed) has depth and height −1.
In the picture below you see a binary tree with height 3 and size 9.
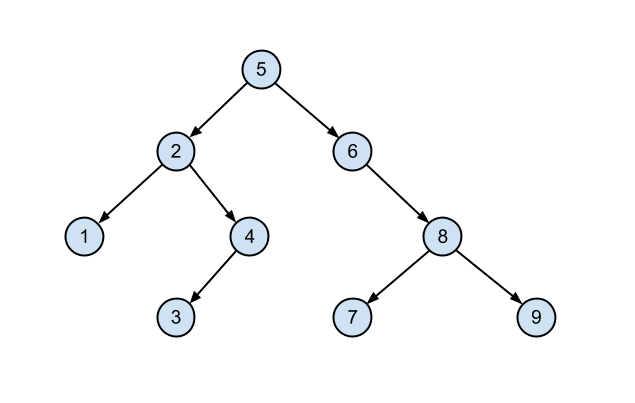 |
| Binary Tree |
int heightOfBinaryTree(BinaryTree node) {
if (node == null) {
return -1;
} else {
return 1 + Math.max(heightOfBinaryTree(node.left),
heightOfBinaryTree(node.right));
}
}
The size solution is recursive, too:
int binaryTreeSize(BinaryTree node) {
if (node == null) {
return 0;
}
return (binaryTreeSize(node.left) + binaryTreeSize(node.right) + 1);
}
ReplyDeleteNice Post!Thanks!
Data Structure Programming Help